要旨
古典拡散の代表であるブラウン運動を行う粒子群の時間発展はガウス分布により記述される。また、気体分子の熱ゆらぎはマクスウェル分布に従う。マクスウェル分布は 3 次元に拡張されたガウス分布と等価である。ガウス分布は中心極限定理が成り立つこと、またスケール変換に対して不変な分布であることから、ゆらぎを持つさまざまな系の統計的記述を行う際に基本となる分布である。
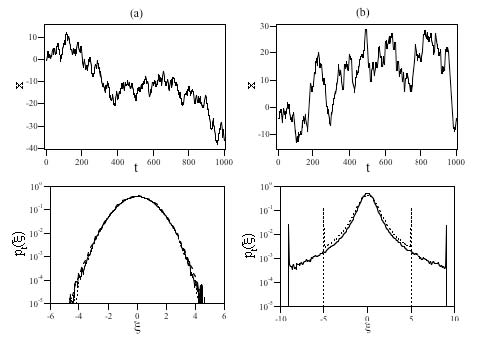
しかし、スケール変換にたいして不変な分布はガウス分布以外にも存在する。それはガウス分布の拡張であるレヴィ分布である。レヴィ分布は非平衡・非線形現象を記述する分布として近年注目されている。レヴィ分布は特性指数が 2 以下でガウス分布より裾野の広いベキ乗分布である。レヴィ分布に従うランダム・ウォークはレヴィ飛翔やレヴィ歩行として知られている。たとえば、渦とジェット流が形成された回転水槽中に浮かべられたトレーサー粒子は、渦による捕捉やジェット流による輸送を繰り返しレヴィ歩行となる。下図にレヴィ分布より生成した粒子軌道の時系列(上段)と、異なる時間スケールでの粒子位置のスケーリングされた分布関数(下段)を示す。古典拡散 (a) に比べ、非古典拡散 (b) での分布関数はスケール変換にたいして不変であるがガウス分布とは明らかに異なりことがわかる。
宇宙空間のプラズマは熱的非平衡状態にあることが多く、レヴィ統計が有用であると考える。本発表では、数値計算より得られる 2 次元磁場ゆらぎ中における高エネルギー荷電粒子の運動が、レヴィ統計により記述されることを報告する。粒子は、散乱体である磁場ゆらぎ構造の自己相似性を反映し、非古典的となる。このとき粒子軌道は、多重スケールの磁場ゆらぎ構造による捕捉(停滞)と非捕捉(歩行)をランダムに繰り返すレヴィ歩行となる。


